Gravitational wave production#

Importing the modules#

[1]:

#start by importing the controller and manipulate modules
from analytical.controller import *
from numerical.manipulate import *
#reimport numpy (though it is pulled by numerical) for smarter syntax highlighting in vscode
import numpy as np
#import matplotlib too
import matplotlib.pyplot as plt

The Standard Model, reproducing the results of 2004.11392 #

The relevant part of the config file is as follows

[Model]
modelpath = /Users/jacopo/NextCloud/AUTOTHERM/autotherm/analytical/models/symmetric_grav.fr
# Symbol for the Lagrangian in the model file
lagrangian = Ltot
# "Name" of the particle whose production rate must be computed
produced = T[1]
# List of the particles in the thermal bath (or leave empty for SM assumption)
# Unused for now, but still required.
assumptions = Element[ht,Reals], Element[kappa,Reals]
replacements =
includeSM = yes
noneq = kappa
flavorexpand =

[ ]:

GWdict=analytical_pipeline("../../MyModels/grav/grav.cfg")

[38]:

from IPython.display import display, Markdown
out=""
s = sympy.Symbol("s")
t = sympy.Symbol("t")
u = sympy.Symbol("u")
g1 = sympy.Symbol("g1")
g2 = sympy.Symbol("g2")
g3 = sympy.Symbol("g3")
ht = sympy.Symbol("ht")
kappa=sympy.Symbol("kappa")
for key, item, in GWdict[0].items():
    sitem=sympy.simplify(sympy.sympify(item).subs(2*t*u,(s*s-t*t-u*u)))
    sitemsubst= sitem
    sitemsubstcollect=0
    for exprtemp in sympy.factor(sitemsubst.expand().as_independent(ht)).subs(t+u,-s)\
        .subs(2*t*t+2*t*u,2*t*t+(s*s-t*t-u*u)).subs(t*t+2*t*u,t*t+(s*s-t*t-u*u)).subs(t*t+t*u,t*t+(s*s-t*t-u*u)/2):
        sitemsubstcollect += exprtemp.simplify()
        # beautify the output
    out+=f"- statistics: {key}:  $${sympy.latex(sitemsubstcollect).replace('ht^{2}',r'\vert h_t\vert^2')}$$\n"
    # display(sympy.pprint(sitem))
display(Markdown(out))

statistics: (1, -1, -1):

\[6 \vert h_t\vert^2 \kappa^{2} s + \frac{2 \kappa^{2} \left(t^{2} + u^{2}\right) \left(5 g_{1}^{2} + 9 g_{2}^{2} + 24 g_{3}^{2}\right)}{s}\]
statistics: (-1, -1, 1):

\[- 6 \vert h_t\vert^2 \kappa^{2} t - \frac{2 \kappa^{2} \left(s^{2} + u^{2}\right) \left(5 g_{1}^{2} + 9 g_{2}^{2} + 24 g_{3}^{2}\right)}{t}\]
statistics: (-1, 1, -1):

\[- 6 \vert h_t\vert^2 \kappa^{2} u - \frac{2 \kappa^{2} \left(s^{2} + t^{2}\right) \left(5 g_{1}^{2} + 9 g_{2}^{2} + 24 g_{3}^{2}\right)}{u}\]
statistics: (1, 1, 1):

\[\frac{\kappa^{2} \left(g_{1}^{2} + 15 g_{2}^{2} + 48 g_{3}^{2}\right) \left(s^{2} + t^{2} + u^{2}\right)^{2}}{4 s t u}\]

[9]:

GW=NumRate(*GWdict,2)
GW.get_leadlog()

[9]:

$\displaystyle \frac{T^{3} \kappa^{2} \left(11 g_{1}^{2} \log{\left(\frac{24 k^{2}}{11 T^{2} g_{1}^{2}} \right)} + 33 g_{2}^{2} \log{\left(\frac{24 k^{2}}{11 T^{2} g_{2}^{2}} \right)} + 96 g_{3}^{2} \log{\left(\frac{2 k^{2}}{T^{2} g_{3}^{2}} \right)}\right)}{192 \pi}$

make the masses explicit

[12]:

md1 = sympy.Symbol("m_{D1}^2")
md2 = sympy.Symbol("m_{D2}^2")
md3 = sympy.Symbol("m_{D3}^2")
T = sympy.S("T")
GW.get_leadlog().subs(g1*g1,6*md1/(11*T**2)).subs(g2*g2,6*md2/(11*T**2)).subs(g3*g3,md3/(2*T**2)).simplify()

[12]:

$\displaystyle \frac{T \kappa^{2} \left(m_{D1}^2 \log{\left(\frac{4 k^{2}}{m_{D1}^2} \right)} + 3 m_{D2}^2 \log{\left(\frac{4 k^{2}}{m_{D2}^2} \right)} + 8 m_{D3}^2 \log{\left(\frac{4 k^{2}}{m_{D3}^2} \right)}\right)}{32 \pi}$

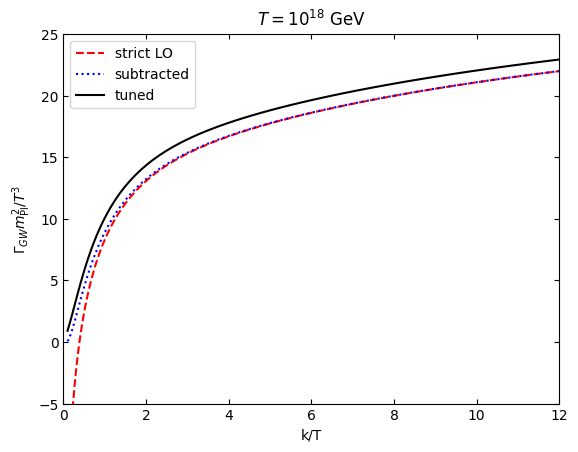
Illustration plot at a very high temperature

[6]:

k=numpy.logspace(numpy.log10(0.1),numpy.log10(12.),100)
GWtestrate = GW.rate(k,numpy.sqrt(32*numpy.pi),(numpy.sqrt(0.172942),numpy.sqrt(0.255890),numpy.sqrt(0.235984),\
                                                numpy.sqrt(0.152066)),0)

[30]:

GW.get_coeffs()

[30]:

{(1, -1, -1): [0,
  -12*ht**2*kappa**2,
  kappa**2*(20*g1**2 + 36*g2**2 + 96*g3**2),
  0],
 (-1, -1, 1): [kappa**2*(20*g1**2 + 36*g2**2 + 96*g3**2),
  kappa**2*(10*g1**2 + 18*g2**2 + 48*g3**2 + 6*ht**2),
  0,
  kappa**2*(20*g1**2 + 36*g2**2 + 96*g3**2)],
 (-1, 1, -1): [0,
  kappa**2*(10*g1**2 + 18*g2**2 + 48*g3**2 - 6*ht**2),
  0,
  kappa**2*(-10*g1**2 - 18*g2**2 - 48*g3**2 - 6*ht**2)],
 (1, 1, 1): [kappa**2*(-g1**2 - 15*g2**2 - 48*g3**2),
  0,
  kappa**2*(-g1**2 - 15*g2**2 - 48*g3**2),
  0]}

[7]:

plt.rcParams['ytick.right'] = True
plt.rcParams['ytick.labelright'] = False
plt.rcParams['ytick.left'] = plt.rcParams['ytick.labelleft'] = True
plt.rcParams["xtick.top"] =  True
plt.rcParams['xtick.direction']='in'
plt.rcParams['ytick.direction']='in'
plt.plot(k,GWtestrate[1],"r--",label="strict LO")
plt.plot(k,GWtestrate[2],"b:",label="subtracted")
plt.plot(k,GWtestrate[3],"k",label="tuned")
plt.xlim(0,12)
plt.ylim(-5,25)
plt.xlabel("k/T")
plt.ylabel(r"$\Gamma_{GW} m_\mathrm{Pl}^2/T^3$")
plt.title("$T=10^{18}$ GeV")
plt.legend()
plt.show()

[8]:

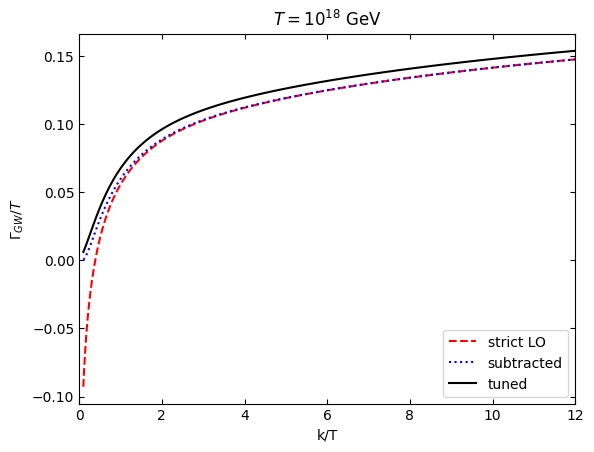
plt.plot(k,10**(2.*18)/((1.2209*10**19)**2)*GWtestrate[1],"r--",label="strict LO")
plt.plot(k,10**(2.*18)/((1.2209*10**19)**2)*GWtestrate[2],"b:",label="subtracted")
plt.plot(k,10**(2.*18)/((1.2209*10**19)**2)*GWtestrate[3],"k",label="tuned")
plt.xlim(0,12)
#plt.ylim(-5,25)
plt.xlabel("k/T")
plt.ylabel(r"$\Gamma_{GW}/T$")
plt.title("$T=10^{18}$ GeV")
plt.legend()
plt.show()

SMASH, reproducing the results of 2011.04731 #

The configuration file is altogether similar to the one above, but points to analytical/models/SMASH_gravity.fr

[ ]:

smashGW=analytical_pipeline("../../MyModels/smashgrav/smashgrav.cfg")

[39]:

from IPython.display import display, Markdown
out=""
s = sympy.Symbol("s")
t = sympy.Symbol("t")
u = sympy.Symbol("u")
yq=sympy.S('yq')
for key, item, in smashGW[0].items():
    sitem=sympy.simplify(sympy.sympify(item).subs(2*t*u,(s*s-t*t-u*u)))
    sitemsubst= sitem
    sitemsubstcollect=0
    for exprtemp in sympy.factor(sitemsubst.expand().as_independent(ht,yq)).subs(t+u,-s)\
        .subs(2*t*t+2*t*u,2*t*t+(s*s-t*t-u*u)).subs(t*t+2*t*u,t*t+(s*s-t*t-u*u)).subs(t*t+t*u,t*t+(s*s-t*t-u*u)/2):
        sitemsubstcollect += exprtemp.simplify()
        # again, beautify output
    out+=f"- statistics: {key}:  $${sympy.latex(sitemsubstcollect).replace('ht^{2}',r'\vert h_t\vert^2').replace('yq',r'\vert y_Q\vert')}$$\n"
    # display(sympy.pprint(sitem))
display(Markdown(out))

statistics: (1, -1, -1):

\[3 \kappa^{2} s \left(2 \vert h_t\vert^2 + \vert y_Q\vert^{2}\right) + \frac{2 \kappa^{2} \left(t^{2} + u^{2}\right) \left(16 g_{1}^{2} + 27 g_{2}^{2} + 84 g_{3}^{2}\right)}{3 s}\]
statistics: (-1, -1, 1):

\[- 3 \kappa^{2} t \left(2 \vert h_t\vert^2 + \vert y_Q\vert^{2}\right) - \frac{2 \kappa^{2} \left(s^{2} + u^{2}\right) \left(16 g_{1}^{2} + 27 g_{2}^{2} + 84 g_{3}^{2}\right)}{3 t}\]
statistics: (-1, 1, -1):

\[- 3 \kappa^{2} u \left(2 \vert h_t\vert^2 + \vert y_Q\vert^{2}\right) - \frac{2 \kappa^{2} \left(s^{2} + t^{2}\right) \left(16 g_{1}^{2} + 27 g_{2}^{2} + 84 g_{3}^{2}\right)}{3 u}\]
statistics: (1, 1, 1):

\[\frac{\kappa^{2} \left(g_{1}^{2} + 15 g_{2}^{2} + 48 g_{3}^{2}\right) \left(s^{2} + t^{2} + u^{2}\right)^{2}}{4 s t u}\]

If we subtract off the SM contribution we have

[36]:

out=""
s = sympy.Symbol("s")
t = sympy.Symbol("t")
u = sympy.Symbol("u")
for key, item, in smashGW[0].items():
    sitem=sympy.sympify(item).subs(2*t*u,(s*s-t*t-u*u)).simplify()
    sitemSM=sympy.sympify(GWdict[0][key]).subs(2*t*u,(s*s-t*t-u*u)).simplify()
    diff=sympy.simplify((sitem-sitemSM))
    diffcollect=0
    for exprtemp in sympy.factor(diff.expand().as_independent(ht,yq)).subs(t+u,-s)\
        .subs(2*t*t+2*t*u,2*t*t+(s*s-t*t-u*u)).subs(t*t+2*t*u,t*t+(s*s-t*t-u*u)).subs(t*t+t*u,t*t+(s*s-t*t-u*u)/2):
        diffcollect += exprtemp.simplify()
    out+=f"- statistics: {key}: $${sympy.latex(diffcollect).replace('yq',r'\,\vert y_Q\vert')}$$\n"
    # display(sympy.pprint(sitem))
display(Markdown(out))

statistics: (1, -1, -1):

\[3 \kappa^{2} s \,\vert y_Q\vert^{2} + \frac{2 \kappa^{2} \left(g_{1}^{2} + 12 g_{3}^{2}\right) \left(t^{2} + u^{2}\right)}{3 s}\]
statistics: (-1, -1, 1):

\[- 3 \kappa^{2} t \,\vert y_Q\vert^{2} - \frac{2 \kappa^{2} \left(g_{1}^{2} + 12 g_{3}^{2}\right) \left(s^{2} + u^{2}\right)}{3 t}\]
statistics: (-1, 1, -1):

\[- 3 \kappa^{2} u \,\vert y_Q\vert^{2} - \frac{2 \kappa^{2} \left(g_{1}^{2} + 12 g_{3}^{2}\right) \left(s^{2} + t^{2}\right)}{3 u}\]
statistics: (1, 1, 1):

\[0\]

The contribution from the BSM Yukawa $y_Q$ agrees with that of 2011.04731. Its contribution through U(1) and SU(3) interactions also agrees

The thermal masses agree with 2011.04731

[20]:

smashGW[2]

[20]:

('(35*g1^2)/18', '(11*g2^2)/6', '(13*g3^2)/6')

and the leading-log term has the usual form in terms of the masses

[22]:

smashGWrate=NumRate(*smashGW,2)
smashGWrate.get_leadlog().subs(g1*g1,18*md1/(35*T**2)).subs(g2*g2,6*md2/(11*T**2)).subs(g3*g3,6*md3/(13*T**2)).simplify()

[22]:

Gravitational wave production#

Importing the modules#

The Standard Model, reproducing the results of 2004.11392#

SMASH, reproducing the results of 2011.04731#

This Page

The Standard Model, reproducing the results of 2004.11392 #

SMASH, reproducing the results of 2011.04731 #